Греки опционов
Торгуя опционами, мы совершаем операции с возможностью осуществления сделки в будущем. При этом оценить, сколько должна стоить данная возможность в текущем моменте, может быть достаточно сложно, а спрогнозировать изменение стоимости данной возможности в дальнейшем – ещё сложнее. Цену опциона определяет ряд факторов: цена базового актива, волатильность, количество дней до экспирации опциона и процентная ставка (для российского рынка значима в меньшей степени). Существуют особые зависимости, которые помогают понять, сколько будет стоить опцион при изменении какого-либо из этих параметров. Количественно выражают эти зависимости следующими буквами греческого алфавита (греками).
- Дельта (Delta) – влияние изменения стоимости базового актива на цену опциона.
- Гамма (Gamma) – скорость изменения дельты при изменении цены базового актива (применяется крайне редко).
- Вега (Vega) – влияние изменения волатильности на стоимость опциона.
- Тэта (Theta), или временной распад, характеризует изменение опционной премии за один день.
Греки опционов помогают прогнозировать как изменение цены отдельно взятого опциона, так и комплексной опционной позиции. Разберёмся в этой теме более подробно.
Дельта
Дельта является коэффициентом перехода изменения цены базового актива в опционную премию. Дельта коллов изменяется от 0 до 1, а дельта путов – от 0 до -1. Причём эти изменения происходят достаточно плавно: за шаг цены страйк в среднем на 0,1 (2500 пп, на примере фьючерса на Индекс РТС и аналогичных опционах). Фактически, если дельта равна 1, значит, изменение цены фьючерса на 1000 пп принесёт изменение опционной премии на аналогичную стоимость: 1000 * 1= 1000. А если дельта равна 0,5, то 1000 пп движения по базовому активу сдвинут опцион лишь на 500 пп: 1000 * 0,5 = 500.
Дельту ещё называют коэффициентом вероятности выхода опциона в деньги. То есть когда опцион находится на деньгах, то его дельта равна 0,5 (-0,5 для путов). Опцион на деньгах то чуть «нырнёт» в деньги, то чуть выйдет из денег. У него достаточно шаткое положение. По сути, решается, пойдёт ли рынок в сторону опциона на деньгах или нет. И вероятность этого движения равна 0,5: либо да, либо нет.
Если опцион находится уже глубоко в деньгах, то при движении фьючерса на 1000 или 500 пп эти пункты переходят в опцион, так как даже при отсутствии ликвидности на страйке мы можем просто исполнить его. А вероятность выхода опциона в деньгах в деньги на момент экспирации – очень большая (возможно, конечно, и резкое обратное движение, способное оставить опцион «за бортом», но оно маловероятно).
А вот опционы вне денег почти дельтой не обладают. Их дельта приблизительно равна 0. Уходит в сторону 0 в среднем на -0,1 при движении из денег на шаг страйка. Представьте, как может измениться стоимость права приобретения актива по очень завышенной цене, куда актив вряд ли дойдёт в принципе, если он чуть дернулся, скажем, на 1000 пп? Логично, что стоимость этого права почти не изменится, разве что на какие-то минимальные значения. Поэтому дельта опционов вне денег очень мала и по мере дальнейшего выхода продолжает падать, максимально приближаясь к 0.
Показывает, как изменится стоимость опциона при изменении волатильности. Но почему волатильность влияет на стоимость опциона? Предположим, есть два актива, которые меняются в цене одинаково, закрываясь каждый следующий день на 1 руб. дороже предыдущего закрытия. Но второй актив, помимо прочего, в течение дня показывает максимальную и минимальную цены с отклонением от предыдущего закрытия в 10 руб. То есть диапазон внутридневных колебаний второго актива – 20 руб. Первый актив меняется линейно: час прошёл – плюс 10 коп., и так вплоть до закрытия на 1 руб. от предыдущего в плюс. Если у нас есть опцион на право покупки актива по 100 руб., то в первом активе нам нужно ждать десять дней, чтобы цена достигла хотя бы цены страйк, и ещё десять дней, чтобы исполнение опциона принесло прибыль. Во втором случае уже на внутридневных колебаниях первого дня цена достигает указанного страйка 100 руб., а на десятый день можно исполнить опцион и получить 9 руб. прибыли. Получается, что прибыль во втором активе зарабатывается быстрее при одной и той же схеме изменения цен закрытия, но при разной волатильности инструментов. А деньги на оставшиеся дни во втором активе можно реинвестировать как минимум под процентную ставку и получить дополнительный доход. Таким образом, рост волатильности увеличивает стоимость опциона, так как искомая прибыль может зарабатываться быстрее на волатильных инструментах.
Вега отражает изменение стоимости опциона при изменении волатильности. В большей степени она влияет на временную стоимость опциона, а не на базовую. Так как если у опциона есть базовая стоимость (например, глубоко в деньгах), то её можно получить, исполнив опцион. Самая большая вега у опционов на деньгах, так как они обладают максимальной временной стоимостью. Минимальной вегой обладают опционы в деньгах, так как влияние волатильности на базовую цену невелико – на опционы в деньгах влияет изменение цены базового актива и дельта. Опционы вне денег тоже обладают минимальной вегой.
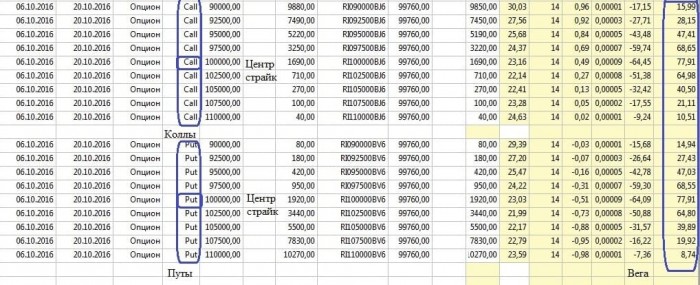
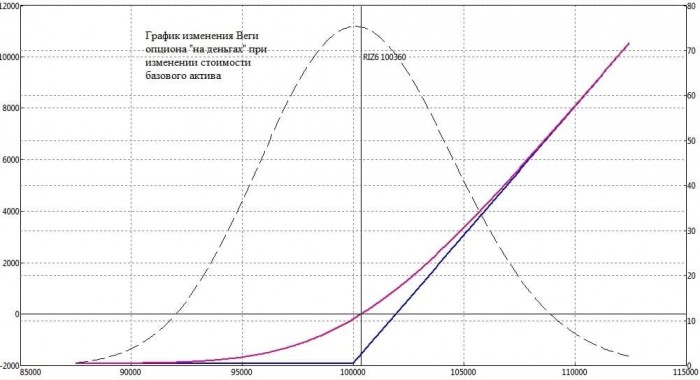
Тэта (временной распад)
Тэта показывает, как изменится цена опциона за день. Так как опционы неминуемо движутся во времени к дате своей экспирации, то их стоимость постоянно сокращается на величину временного распада. Тэта оказывает влияние только на временную стоимость. Базовую стоимость тэта сократить не может, так как в американских опционах есть возможность исполнения до даты экспирации. Тэта имеет максимальные значения для опционов на деньгах, обладающих максимальной временной стоимостью. Для опционов вне денег и на деньгах тэта снижается.
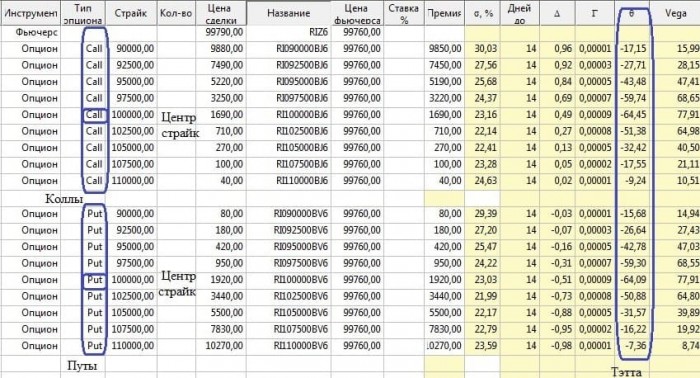
Тэта является нелинейным параметром. И если сравнить опционы текущей и следующей экспирации, то их стоимость не будет пропорционально равной. Таким образом, один день владения опционом дальнего срока экспирации с точки зрения временного распада окажется более дешёвым.
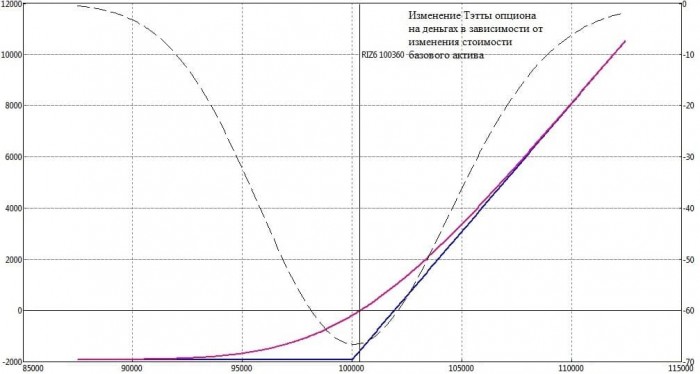

В комплексных конструкциях, образованных множеством опционов, греки опционов суммируются, и сами конструкции изменяются в стоимости в соответствии с просуммированными греками.
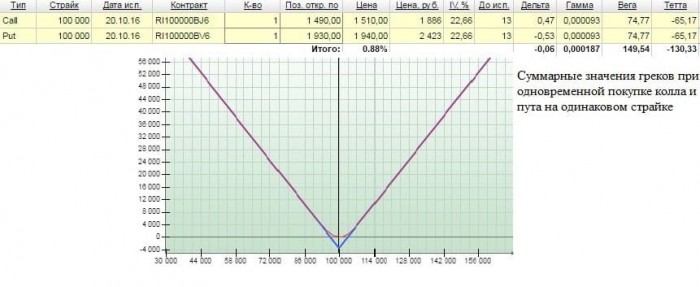
Например, при покупке колла и пута на одном и том же страйке происходит суммирование греков опционов. В частности, дельта колла равна 0,47, а пута —0,53. Сумма дельты равна —0,06. То есть конструкция образована противоположными дельтами, суммарная дельта практически нулевая. Получается так, что при росте базового актива, например, свыше 3500 пп от текущего значения образуется прибыль, так как пут обесценивается, а колл успевает своим ростом покрыть и свою стоимость, и стоимость пута. Если же рынок снижается на 3500 пп, то колл обесценивается, а пут, дорожая, перекрывает затраты на колл и на своё приобретение. Получается, куда бы рынок не пошёл с исходной околонулевой дельты, образуется прибыль, даже если рынок пройдёт хотя бы 3500 пп. Подобного рода конструкции называются дельта-нейтральными.
Греки опционов помогают прогнозировать изменение стоимости как единичных опционов, так и комплексных опционных конструкций, определяя специфику получения прибыли. Опционы способны приносить весомый доход и страховать риски биржевых торгов, а понимание греков позволяет использовать опционы максимально эффективно.
Остались вопросы? Напишите нам через форму обратной связи или оставьте заявку. Помочь разобраться в нюансах, связанных с торговлей опционами, и максимизировать прибыль вам всегда поможет «Открытие Брокер»!
Понравилась статья? А у нас таких много! Подписывайтесь на еженедельную рассылку – и подборки самых актуальных, полезных и интересных материалов будут еженедельно приходить прямо на вашу электронную почту!
Гамма (γ)
В мире финансов гамма означает скорость изменения дельты. Более конкретно это понятие используется при обсуждении опционов. Гамма для опционов записывается в виде процентного значения. Она представляет собой изменение дельты опциона при каждом однопунктовом изменении цены базовой акции.
Гамма постоянно меняется, даже когда цена акции движется незначительно. Гамма наиболее близка к своему пику, когда цена акции близка к цене исполнения опциона. Стоимость опциона — и, следовательно, гамма опциона — уменьшается по мере того, как опцион все дальше уходит от денег.
Резюме:
- Гамма — это производная греческой метрики, измеряющая скорость изменения дельты.
- Гамма — одна из четырех общепринятых метрик для оценки риска при работе с опционами. Также используются дельта, вега и тета.
- Длинные опционы имеют положительную гамму при росте цены; короткие опционы имеют отрицательную гамму при снижении цены.
Четыре показателя
Существуют четыре общепринятые метрики для оценки риска, когда речь идет о позициях по опционам на акции. Эти четыре метрики, обычно называемые «греками», являются ключевыми показателями, о которых должны знать трейдеры опционов, даже те, кто не использует греческие числа при принятии торговых решений. К четырем показателям, о которых важно знать всем трейдерам, относятся:
1. Дельта
Дельта измеряет изменение премии опциона в зависимости от того, как изменяется цена базовой ценной бумаги. Для дельты значения варьируются от -100 до 0 (путы) и от 0 до 100 (коллы). Она дает возможность прогнозировать изменения цены опциона на основе корреляции опциона с ценой базового актива.
Например, если дельта опциона равна 50, то теоретически стоимость опциона будет увеличиваться на 50 центов на каждый один доллар роста цены базовой акции. Дельта также рассматривается как метрика вероятности. Дельта в 0,50 интерпретируется как вероятность того, что опцион будет в деньгах в момент истечения срока его действия, примерно 50/50.
2. Гамма
Гамма — это метрика для измерения изменений дельты за определенный период времени. Значения дельты регулярно меняются по мере колебания цены базового актива. Гамма полезна тем, что помогает трейдерам увидеть скорость изменений и их влияние на стоимость и премии опционов. Это может помочь им в дальнейшем прогнозировании возможных будущих движений цен.
Гамма опциона выражается в процентах. Значение гаммы опциона, как и стоимость самого опциона, снижается по мере приближения срока действия опциона.
3. Тета
Тета измеряет, как снижается временная стоимость опциона на протяжении всего срока его действия (временной распад). С каждым прошедшим днем потенциал прибыльности опциона снижается. Чем ближе к дате истечения срока действия опциона, тем быстрее скорость распада. В последние недели перед истечением срока опциона скорость, с которой опцион теряет временную стоимость, ускоряется.
4. Вега
Вега — это метрика подразумеваемой волатильности. Другими словами, вега измеряет влияние изменений волатильности базового актива на цену/стоимость опциона. В частности, он отражает влияние на опционы каждого 1%-го увеличения или уменьшения волатильности базового актива. Уровень волатильности базового актива обычно оказывает большое влияние на цены опционов.
Более высокая волатильность обычно означает более высокие опционные премии, в то время как более низкая волатильность приводит к более низким премиям. Многие опционные трейдеры стремятся покупать опционы в периоды низкой волатильности и продавать их в периоды высокой волатильности, чтобы максимизировать прибыль.
Гамма в модели Блэка-Шоулза
Использование греческих метрик было популяризировано в модели Блэка-Шоулза, которая является финансовой моделью, предоставляющей информацию о динамике финансового рынка, в частности, когда используются производные инвестиционные инструменты.
Гамма и другие греческие метрики помогают показать, насколько чувствительна стоимость производных инструментов к изменениям стоимости базового актива. Гамма, как отмечалось выше, сама является производной от одного из других греческих метрик — дельты.
Опционы колл обычно имеют плюсовую, или положительную гамму, в то время как опционы пут обычно имеют отрицательную гамму.
Дополнительные ресурсы:
Портал Finansistem поможет любому человеку стать финансовым аналитиком мирового класса. Для дальнейшего развития вашей карьеры вам будут полезны дополнительные ресурсы, представленные ниже:
Опционы для начинающих. Гамма

Если по-научному, то гамма это вторая производная цены опциона.
Ага, осталось вспомнить что такое производная.
Если по проще, то производная это скорость. Т.е. дельта (первая производная) — это скорость изменения цены опциона от изменения цены БА, а гамма – это скорость изменения дельты опциона (т.к. она вторая производная) от изменения цены БА. Получается, что гамма – это ускорение цены опциона в данной точке БА.
Сейчас БА = 100000
Опцион колл со страйком 102500 и дельтой 0.45
БА смещается на 100пп. И его дельта станет уже 0.454
В переводе на «фьючерсный» язык – наша позиция выросла в лотах.
Наша позиция «спирамидилась», но не дискретно (как если бы мы просто докупили один лот), а плавненько с каждым пунктом цены БА.
Теперь нам нужно все это как-то представить графически. Мы должны понимать, что будет не только с ценой опциона через х-пунктов, но и с дельтой, и с гаммой.
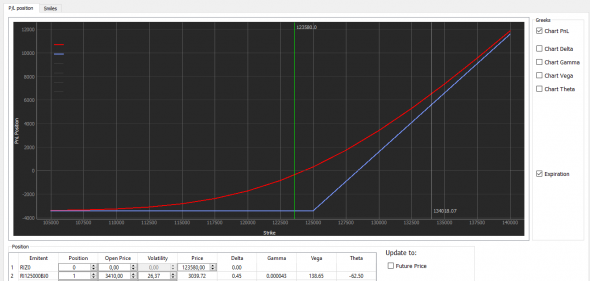
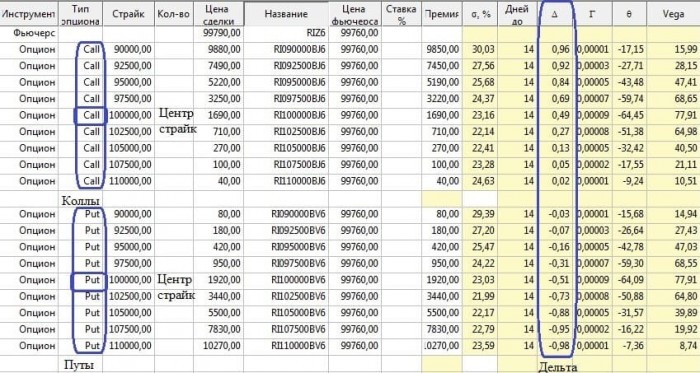
Для этого берем аналитик и «закидываем» в него опцион колл на центральном страйке:
Как мы видим, дельта такого опциона 0.45, а гамма 0.000043
Это значит, что наша дельта будет изменяться с каждым шагом БА на 0.000043. Вроде и не много. Но. Во-первых, посчитайте, что будет с дельтой через 1000-2000 пунктов. Для фьюча на РТС это норма дня.
Дельта = 0.45 + 0.000043 х 2000 = 0.45 + 0.086 = 0.536
Дельта изменилась на 19%
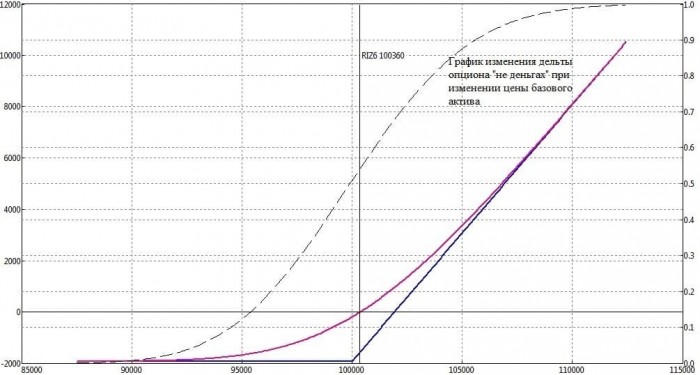
Такой подсчет, конечно, очень грубый. Т.к. гамма тоже будет меняться в зависимости от цены БА. Вот чтобы совсем не сойти с ума от таких изменчивых параметров – есть в аналитиках графическое представление:
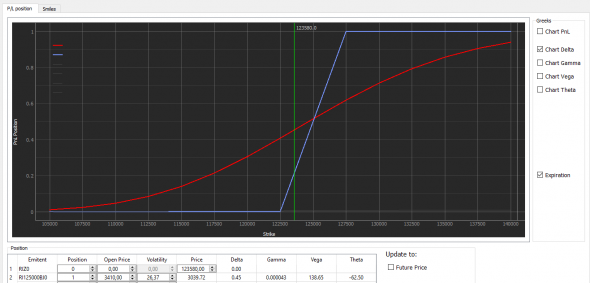
Вот тут наглядно видно, как меняется дельта. Совсем не линейно и не одинаково. Это как раз и подтверждает, что гамма тоже не линейна:
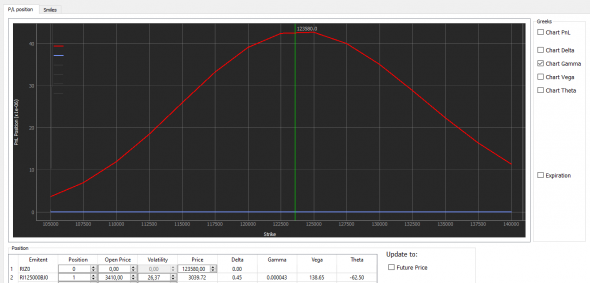
Хорошо видно, что когда опцион на деньгах, то гамма максимальна. И чем дальше цена от страйка, тем больше гамма стремится к нулю. А все потому что опцион превращается либо в ноль с нулевой дельтой. Либо во фьючерс с дельтой 1. И в первом и во втором случае его дельта перестанет изменяться и скорость (гамма) стремится к нулевому значению.
Данные графики приведены для одного купленного колла. Так редко кто торгует. Чаще собирают различные конструкции из опционов. Там графики для каждого опциона и фьючерса будут складываться и получатся совершенно другие картины:
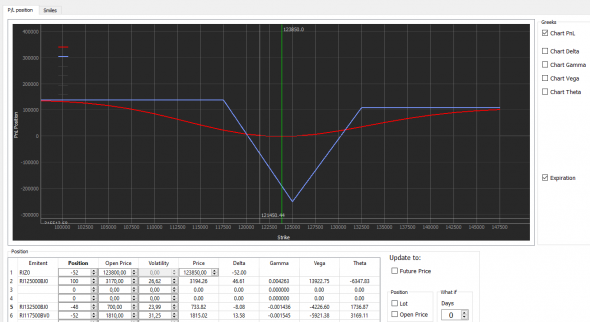
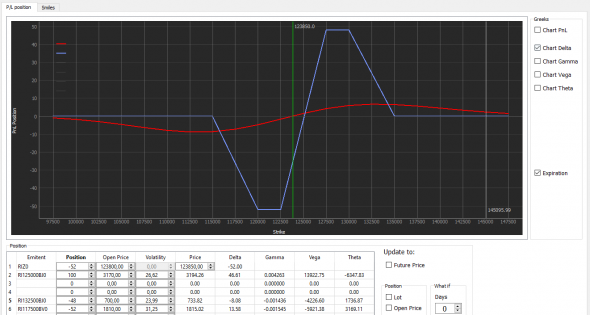
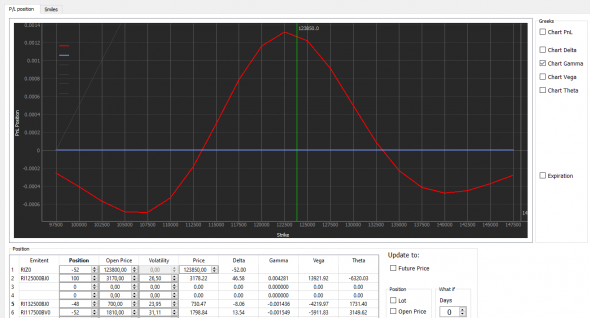
Обратите внимание – там, где у нас дельта нейтральна (равна нулю), там гамма тоже равна нулю, но стоит чуть БА пройти в сторону, гамма тут же увеличивается (по модулю) и дельта так же нарастает (тоже по модулю).
А еще гамма может быть отрицательной – тогда дельта будет изменяться противоположно БА. Например:
Дельта положительная, а гамма отрицательная – при росте БА, дельта будет падать.
Дельта отрицательная, гамма отрицательная – при падении БА, дельта будет стремиться к нулю, т.е. уменьшаться по модулю.
В следующих уроках мы не раз будем использовать гамму в своих расчетах позиций.
Источник https://journal.open-broker.ru/trading/greki-opcionov/
Источник https://finansistem.com/gamma/
Источник https://smart-lab.ru/blog/646840.php